Yay! So you've figured out how to parallelize your problem, and you have a bunch of workers. Splitting up the work should be pretty simple right? Well, sometimes it's not. Recognize a theme here? If you haven't figured out yet that the never truly is something "Simple" in the dev world, that there is always a caveat or 5 other ways to do it, well... welcome!

So, lets go back to the Mandelbrot problem to take a look at what we are dealing with.

There are many ways to divide work between your worker pool. The best choice depends on the environment of the problem space, and the requirements of the solution.

The first two are by far the simplest. They involves splitting the work evenly across your worker pool before you get started. They are perfect for when you know your work ahead of time, AND when all the pieces of work are of equivalent size.

Chunking

Chunking is just like it sounds: Splitting the work evenly into chunks. So if I have 2 workers, the 1st worker takes the 1st half of the work and the 2nd worker takes the 2nd half. This is simple to scale really. If you have n workers, you divide the work into n chunks, and then the workers do the work and they are done, right? Well, without going into the math behind the Mandelbrot set, consider the fact that the rows of pixels that have more black than blue in the picture above, take more work than the others. More black, more work. So, with 2 workers, the work would in fact be divided pretty evenly, top and bottom. But say we had more. Well the workers with the top and bottom chunks would have less work than the workers in the middle. So they would finish first, and be doing nothing. This doesn't seem like the best way to go, does it?

Striping

Striping is slightly different. If I have two workers, the first worker gets the first row, the second worker gets the second row, the first worker gets the third row, and so on. This scales to n workers, as each worker gets a stripe. With the Mandelbrot set, this seems like a good solution. However, it might not be the best solution for all problems. What if we don't have all our problem space at the very beginning. What if the problem space grows as we compute? What if the problem space is cyclical, and we have the bad luck of choosing a worker pool size that harmonizes with the cycle? That means if the nth job is the hardest, the nth worker will always get the most work.

There are ways around this.

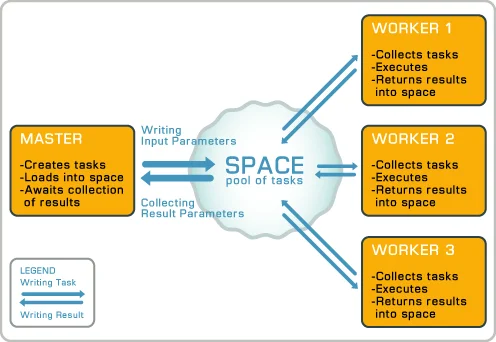
Master / Worker

A Master / Worker paradigm involves two distinct sets of processes. The master manages the work pool. It inserts tasks for work, and the workers process the tasks waiting to be done. So, in the case of the Mandelbrot problem, the Master would assign n tasks out to n workers. When a worker reported back with the results of their work, the Master process would assign them another task. This would go on and on until the work was done. If the results represented partial results, the Master would be the one to combine the work all together. With Chunking and Striping, there actually still is a Master process. With the Mandelbrot problem for instance, each worker would return the values of the rows, but the Master would be the one to stitch all the rows together into a final image. Work can be assigned as it's done, as I describe in this section, or all at once with some sort of partitioning scheme.

I don't know about you, but the master process seems like it's a waste of space, especially in a real time environment.

Agnostic

If we can have our work producers, the web clients, mobile apps, api servers, whoever is producing work, produce it in an acceptable work "package", we can queue it up in a way that the workers can divide the work up themselves, without a master process.

This is a common paradigm in cloud infrastructure: asynchronous workers wait for work to be, and they process the work as it comes in. This is great for tasks that are not time or order sensitive, like sending transactional emails.

The most common way to schedule work for a worker pool like this is using a queue. Queues have been around since the early days of computing. It's like when you go to get a coffee at the Café, you get in the back of the line. It's called a FIFO Queue: First In First Out. When a worker needs work to do it takes the next job of the queue and processes the work. For problems like sending emails, it is independent of the work other workers are doing. However, for building the a Mandelbrot plot, the worker would then need to insert the row into the final result themselves.

This is great. But there are some problems with this. What happens if a worker crashes? The work gets lost. In a future post, we will discuss ways to make a worker queue more reliable and redundant without sacrificing parallelism.

Many minions! Think about it. If you have a ton of work to do, and you want to get it done as quickly as possible, you go sucker a bunch of friends to help you. Welcome to the world of parallelization. Sounds simple right? Well, yes and no.

Lets start out with a simple problem. Remember when your teacher had you switch your quiz with a classmate and grade each other's? They had n tasks to do, and they were able to divide it between n workers. This is a perfect storm. It rarely happens, but it provides a good base line for this discussion.

Embarassingly Parallel

So lets say we want to calculate the curve for a polynomial function:

y=x^2

with this problem, each value has no data dependencies. No value depends on a previous value. So we can give each calculation to a separate worker.

A computer architect by the name of Gene Amdahl came up with a measure for how much speedup you can get by parallelizing a problem. Its called Amdahl's Law.

Given:

P, The proportion of the problem that can run in parallel
N, The number of workers

The speedup is calculated as follows:

S(N)=1/((1-P)+P/N)

So, assuming we have an infinite number of workers, as we parallize more and more of the problem, our speedup also approaches infinite.

for our problem above, let's say our program has a 1% overhead when it comes to dividing up the work. Our speeup with infinite workers would then be:

S(I)=1/((1-.99)+P/I) = 1/.01 = 100

The problem above is whats termed embarassingly parallel.

Not so embarrassing

So what problems are harder? Let's look at the Mandelbrot Set.

Don't worry about understanding the math. The problem with calculating the set is that each value in a row of values is dependent on the value before it in the row. So we have a data dependency. Given a problem space of m columns and n rows, we can only divide he problem into n pieces. That we will cover in a future post.

So I have a ton of minions, now what?